ОСНОВИ КРЕСЛЕННЯ

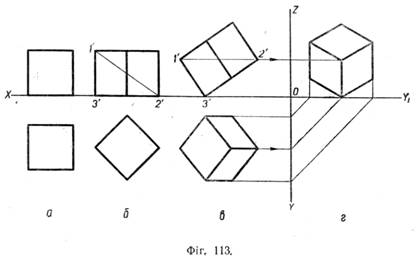
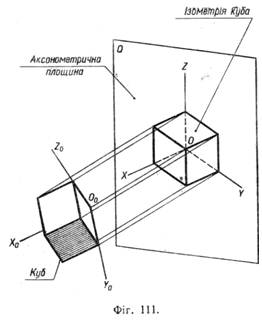
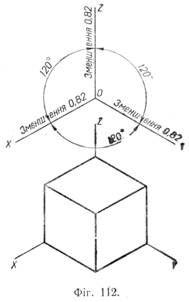
У практиці широко використовується аксонометрична проекція, що називається прямокутною ізометричною, або, скорочено, ізометрією.

В ізометричній прямокутній проекції проектуючі промені перпендикулярні до аксонометричної площини Q (фіг. 111), що становить з кожною з осей координат О0Х0, O0Y0, O0Z0 однакові кути (35°). Проекції осей координат на аксонометричну площину — аксонометричні осі OX, OY і OZ — утворюють одна з одною кути 120° (фіг. 112). Розміри предмета, відкладені вздовж координатних осей, при проектуванні на аксонометричну площину зменшуються в 0,82 раза.

Процес утворення ізометричної проекції можна подати ще й так. На фігурі 113, а дано дві проекції куба (фронтальну і горизонтальну), що стоїть на горизонтальній площині проекцій. При такому положенні куба його проекціями на площині V і H будуть квадрати.

Залишаючи куб стояти на площині Я, повернемо його проти годинникової стрілки на 45° (фіг. 113, б). В новому положенні проекціями куба на площині Я буде, як і раніше, квадрат, а на площині V — прямокутники. Тепер піднімемо основу куба, лишаючи вершину З на площині Я. Підніматимемо куб доти, поки його діагональ 1—2 не стане паралельною площині Я (фіг. 113, в). Після цього на площині Я проекції всіх -граней куба перетворяться в ромби. Якщо тепер побудувати профільну проекцію куба за двома наявними (на фіг. 113, в праворуч), то вийде зображення (фіг. 113, г), що відповідає ізометричній проекції. Зауважимо, що на профільній проекції всі ребра вийшли зменшеними (у 0,82 раза).

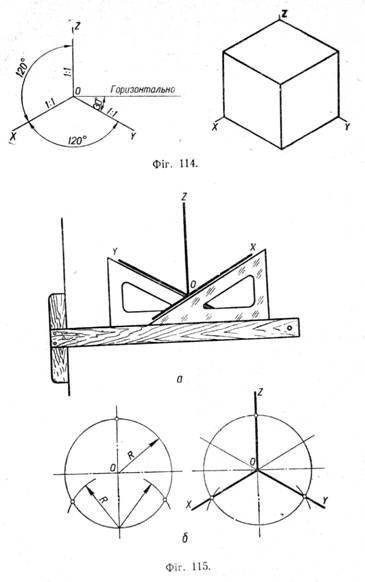
Побудову ізометрії на практиці спрощують тим, що відкладають по осях OX, OY і OZ і паралельно їм натуральні розміри предмета. При цьому виходить дещо збільшене зображення, що, однак, не псує його наочності. Збільшення
зображення становить 1/0.82= 1.22 раза.

На фігурі 114 ізометрія куба побудована за натуральними розмірами. Як видно з порівняння фігур 112 і 114, обидва зображення мають однакову наочність і відрізняються одне від одного тільки величиною.

Ми будуватимемо наочні зображення в ізометрії тільки за натуральними розмірами, як це прийнято на практиці.

На фігурі 115, а показано прийом побудування ізометричних осей за допомогою косинця з кутами 30°—60°—90°, а на фігурі 115, б — за допомогою циркуля.

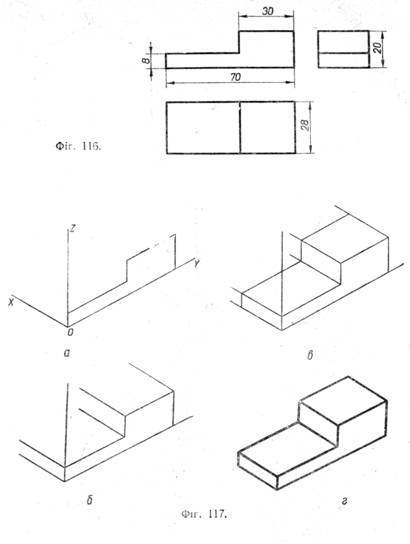
Розглянемо на прикладах прийоми побудування наочних зображень в ізометрії.

Приклад 1. На фігурі 116 наведено креслення планки. Керуючись кресленням, треба побудувати наочне зображення планки в ізометрії.

На фігурі 117 показано послідовність цієї побудови за етапами.

1. Проведено осі ізометрії і в площині ZOY побудовано фігуру, що відповідає на кресленні виглядові спереду (фіг. 117, а).

2. Із вершин цієї фігури проведено прямі, що паралельні осі ОХ (фіг. 117, б).

3. По осі ОХ відкладено ширину деталі (28 мм) і проведено прямі, що паралельні відповідним осям (фіг. 117, в).

4. Усунено зайві лінії,після чого зображення обведено (фіг. 117, г).

Приклад 2. На фігурі 118 наведено креслення правильної шестикутної призми. Керуючись кресленням, треба побудувати наочне зображення призми в ізометрії.

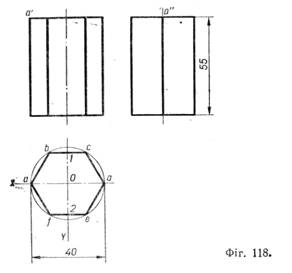
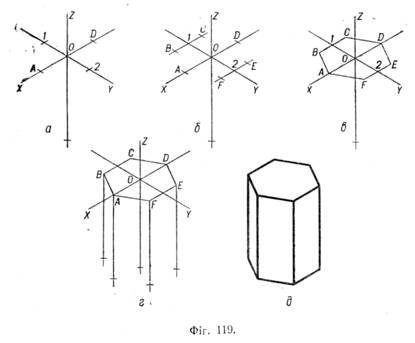
Побудування ізометрії призми за етапами показано на фігурі 119. При цьому фігури 119, а, б і в ілюструють порядок побудування в ізометрії шестикутника (верхньої основи призми).