| Коло в ізометрії |
 |
|
Еліпсом (фіг. 122) називається замкнута плоска крива, що має такі геометричні властивості: сума відстаней будь-якої її точки до двох точок, що називаються фокусами (F і F1) еліпса, є величина стала, що дорівнює великій осі еліпса (АВ). Еліпс має дві осі симетрії: велику вісь АВ і малу CD. Точка перетину осей О називається центром еліпса. Еліпс будують по точках і обводять по лекалу.
При нахилі квадрата на 55°, він перетвориться в ромб, при цьому сторони квадрата скоротяться в 0,82 раза. Величина вертикального діаметра CD скоротиться в 0,58 раза. Таким чином, коло в ізометрії проектується в еліпс, велика вісь якого дорівнює діаметру кола d, а мала вісь еліпса дорівнює 0,58 d. Як відомо, на практиці для спрощення побудов ізометрію будують без зменшення розмірів по осях в 0,82 раза. При цьому зображення виходить збільшеним у 1,22 раза. Креслячи коло в ізометрії без урахування скорочення розмірів по осях, треба розмір великої осі еліпса збільшити до 1,22 d, а малу вісь взяти 0,7 d, де d — діаметр зображуваного кола. Наприклад, для кола діаметром 100 мм велика вісь еліпса буде 122 мм (1,22 • 100 = 122), а мала вісь — 70 мм (0,7 • 100 - 70). Положення еліпсів в ізометрії. Наочне уявлення про можливі положення еліпсів в ізометрії дає фігура 124, на якій показано три циліндри, що примикають своїми основами до верхньої (горизонтальної) і двох бокових (вертикальних) граней куба (зображення циліндричних поверхонь на фігурі 124 для більшої виразності відтінені так званою шрафіровкою).
У циліндрі, що примикає до верхньої грані куба, мала вісь еліпса, як і сама вісь циліндра, розміщені вертикально; велика вісь еліпса — горизонтально.
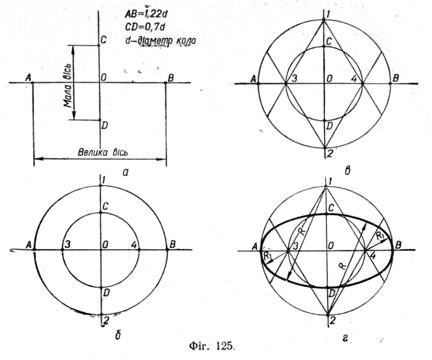
У циліндрі, що примикає до лівої бокової грані куба, мала вісь еліпса, як і сама вісь циліндра, напрямлена вздовж осі X, а велика вісь еліпса їй перпендикулярна. У кресленні допускається для простоти і прискорення побудов креслити замість еліпсів овали, що складені з дуг кіл і дуг, що проводяться по лекалу. 1. Проведено дві взаємно перпендикулярні лінії і відкладено від точки О розміри великої і малої осей еліпса (фіг. 125, а).
4. Із центрів 1 і 2 циркулем проведено дві дуги через точки С і D, а з центрів З і 4 через точки А і В проведено дуги, які замикають овал (фіг. 125, г).
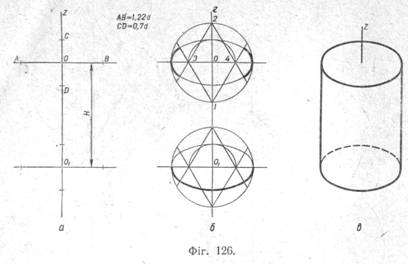
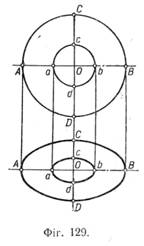
У першій стадії (фіг. 126, а) проведено вісь Z, на якій відкладено відрізок ОО1, що дорівнює заданій висоті циліндра, після чого через точки О і О1 проведено горизонтальні лінії. Далі визначено розміри великої і малої осей еліпса і відкладено від точок О і О1. У другій стадії (фіг. 126, б) побудовано овали основ. У третій — останній стадії (фіг. 126, в)—усунено зайві лінії допоміжних побудов і обведено контури проекції. Для наочності вісь Z показано потовщеною лінією. Звернемо увагу на таку особливість ізометрії двох концентричних кіл (фіг. 129): відрізки Аа і ВЬ більші за відрізки Сс і Dd. |
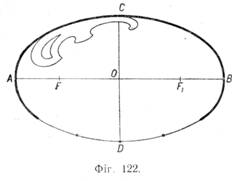 Утворення еліпса. В ізометрії коло може спроектуватись у вигляді кола, відрізка прямої і еліпса.
Утворення еліпса. В ізометрії коло може спроектуватись у вигляді кола, відрізка прямої і еліпса.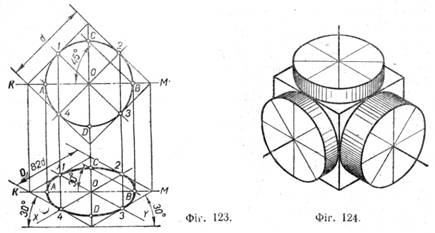
 У циліндрі, що примикає до правої бокової грані куба, мала вісь еліпса, як і сама вісь циліндра, напрямлена вздовж осі Y, а велика вісь еліпса їй перпендикулярна.
У циліндрі, що примикає до правої бокової грані куба, мала вісь еліпса, як і сама вісь циліндра, напрямлена вздовж осі Y, а велика вісь еліпса їй перпендикулярна.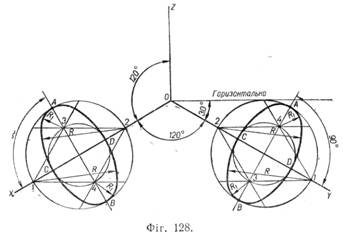
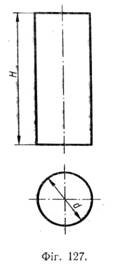
 На фігурі 126 показано послідовність побудови ізометрії циліндра, вісь якого вертикальна, а основи — горизонтальні. Розміри циліндра взято з креслення (фіг. 127).
На фігурі 126 показано послідовність побудови ізометрії циліндра, вісь якого вертикальна, а основи — горизонтальні. Розміри циліндра взято з креслення (фіг. 127).